O Algoritmo de Quake 3 que Revolucionou os Jogos
O Algoritmo do Quake 3 que Revolucionou os Jogos
Contextualizando

A importancia da raiz quadrada no ambinete 3D
O código abaixo exemplifica uma das importância da raiz quadrada para detectar colisões:
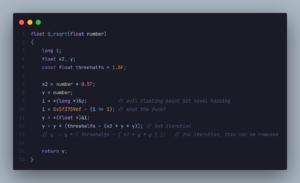
Por dentro do algoritmo
Vamos examinar o algoritmo:
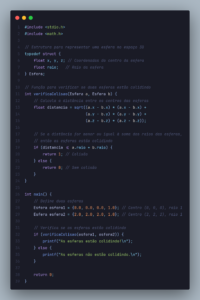
Explorando o algoritmo
Por dentro da matematica
A manipulação de bits é uma técnica fundamental na computação, onde toda a informação é representada por sequências de 0s e 1s, chamadas de bits. Esses bits são agrupados para formar diferentes tipos de dados, como bytes, que são grupos de 8 bits. O primeiro passo do algoritmo é converter o número de ponto flutuante em uma representação binária e, em seguida, manipular os bits desse número para obter uma aproximação rápida da raiz quadrada inversa.
Resumidamente, a manipulação de bits envolve realizar cálculos matemáticos em um nível mais baixo do que as operações aritméticas, alterando diretamente os padrões de 0s e 1s que representam os números. Essa técnica permite manipular os valores de forma eficiente e rápida, o que é especialmente útil em situações onde o desempenho é crítico, como em motores de jogos 3D.
A imagem abaixo exemplifica como a manipulação de bits pode ser usada para realizar operações como deslocamento de bits para a esquerda e para a direita, além de operações lógicas como AND, OR e XOR.
 Nessa imagem, podemos ver como os bits de dois números são manipulados usando diferentes operações de bit a bit para produzir um resultado específico. Essas operações de manipulação de bits são a base para muitos algoritmos eficientes e poderosos na computação.
Nessa imagem, podemos ver como os bits de dois números são manipulados usando diferentes operações de bit a bit para produzir um resultado específico. Essas operações de manipulação de bits são a base para muitos algoritmos eficientes e poderosos na computação.
IEEE 754 e Padrões de Ponto Flutuante: O padrão IEEE 754 é uma especificação fundamental para a representação e aritmética de números em ponto flutuante em sistemas computacionais. Ele define formatos padronizados para representar números em ponto flutuante, além de especificar operações aritméticas para manipular esses números. O IEEE 754 é amplamente adotado em computadores modernos e desempenha um papel essencial na representação e manipulação precisa de números reais em diversas aplicações computacionais.
Aproximação do Logaritmo por 2: Uma das partes essenciais do algoritmo é a aproximação do logaritmo por 2 do número de entrada, expressa em “i = 0x5f3759df – (i >> 1)”. Esse cálculo é realizado por meio de manipulações bit a bit e truques matemáticos. O propósito é simplificar os cálculos subsequentes, tornando-os mais rápidos e eficientes, uma vez que a representação binária de um número está intimamente relacionada ao seu logaritmo na base 2.
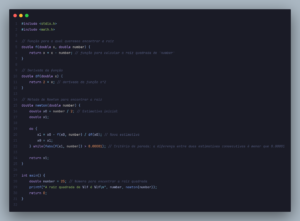
Método de Newton: Também conhecido como Método Newton-Raphson, é uma técnica iterativa amplamente utilizada para encontrar raízes de equações não lineares. Este método é especialmente eficaz quando a derivada da função é conhecida ou pode ser facilmente calculada. Funciona aproximando iterativamente a raiz da função por meio de tangentes à curva da função.
O código a baixo é um exemplo de implementação desse método na linguagem C:








Publicar comentário
Você precisa fazer o login para publicar um comentário.